First introduced by Calabi, and also described by Cheeger in one of his famous papers, these dumbbell-shaped surfaces are a very well studied example in Spectral Geometry. The first eigenvalue of the Laplacian of these surfaces is proportional to the radius of the cylinder joining the two spheres. Thus, considering dumbbells with very thin cylinders, we obtain surfaces with arbitrarily small first eigenvalue.

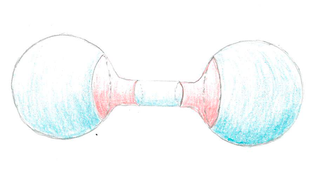
In view of Lichnerowicz's theorem, this example shows that to find a positive lower bound for the first eigenvalue, one needs some kind of curvature assumption. Together with Kamryn Spinelli and Connor C. Anderson, two undergraduate students at Worcester Polytechnic Institute, we have been exploring this example in the context of integral curvature assumptions. Our exploration lead to a joint publication at PUMP Journal of Undergraduate Research, and the students presented our findings at the 2021 MAA MathFest and in the 2022 Joint Mathematics Meeting.

Mathematics can be found everywhere: basic Arithmetic explains us how sales work, Differential Equations explain us how planets orbit around the Sun, Geometry tells us that the Earth is not flat, Combinatorics tells us how many "clinks" will we hear in a toast, Probability tells us how unlikely it is to become rich by buying lottery...

However, sometimes it is hard to explain what Algebra does for us (and here by Algebra I mean actual Algebra); and the truth is that Algebra is beneath every single one of these fields! In this post I want to explain one of my favourite theorems, how its roots are essentially algebraic (although it is a theorem in combinatorics), and how it can be applied to the real world: Pólya enumeration theorem.

Last summer I participated in a summer school on Geometric Analysis in the beautiful town of Como, Italy. A part from having a great time and meeting a lot of mathematicians, I was introduced, by professor Christina Sormani (CUNY), to a new notion of convergence of metric spaces: the Sormani-Wenger Intrinsic Flat Convergence.

What is this all about, you might be asking? Well, before jumping on this rather involved concept, let's try to understand what is a metric space and what do I mean by convergence of metric spaces.

Some time ago, one of my facebook friends posted a quote of a result by Paul Erdös:

If an infinite set of points in the plane determines only integer distances, then all the points lie on a straight line.

When a mathematician reads something like this, after realizing that it is a nice result, the first question that comes to his mind is: is it possible to construct a finite set of n points in the plane that do not lie in a straight line, and whose distances are all integers?

Well, it is easy to see that one can do that for n=3 (just consider any Pythagorean triple, such as the triangle with sides 3, 4, and 5). But is it possible to do that for an arbitrary n? The answer is not obvious at first, unless you have thought about the problem before (although that this is probably a very well established result). Actually, the proof of the statement above, called the Erdös-Anning theorem, was published in 1945, and the proof already contains a solution to the case with finitely many points. However, although beautiful, the example that the paper provides is overcomplicated, from my point of view.

Plus, I didn't know the answer to this question, and I realized that many of my fellows didn't know it either, so I started to try to construct examples of sets of non-aligned points with integer distances between them.

From the example of the triangle, it was easy to construct a set of n=4 points with this property, just by considering the rectangle of sides 3 and 4 (whose diagonal has length 5). But again, being able to do it for n=4 points doesn't mean that it can be done for any number of points, and I didn't see how to generalize that construction.

General Relativity has always fascinated me; it is probably one of the main reasons why I decided to study mathematics and physics, and it is definitely an important reason for studying Differential Geometry and Geometric Analysis, even if my research is not focused in Einstein's equations. Why is it so fascinating? Well, that's what I am going to explain on Friday, in the Graduate Student Seminar (1pm-2pm, Surge 284, UCR). But in case you can not make it, let me explain you a few things about relativity.

Let me be honest with you. When I applied to UCR for my PhD I didn't think I would end up studying here, I didn't know too much about this school, nor about its faculty members. However, the Department of Mathematics in Riverside has a lot of good and worldwide famous mathematicians. Among them, John Baez caught my attention when I applied to UCR, and he is, together with my PhD advisor Qi S. Zhang, the main reason I decided to come here.

John Baez is a very active professor, not only in the university, but also online: in his webpage (one of the first "blogs" in the world wide web) you can find, literally, all sorts of things; I love to get lost surfing through it! He is an awesome instructor, I had the opportunity to attend one of his classes, MATH209A, an introduction to measure theory, and after that I decided to do my best to attend as many of his classes as I could. That's the reason that I have been attending his seminars on Network Theory and on Category Theory!

I have spend a whole week in Oberwolfach, and I must say that it has been an incredible experience! The place is just amazing: a nice complex of buildings in the middle of the Black Forest, designed according to the needs of a center like MFO. In addition to that, I met some incredible people there, and the Seminar was very interesting!

This is the first post in my professional blog! The aim of this blog is to share ideas, discoveries, exciting news, academic experiences, and much more with all of you!

Not only the blog is new, but also, I have build a brand new professional website! You can find there my CV, my contact information, a summary of my research, and my teaching experience. Enjoy!!