Integer distances in the plane

Some time ago, one of my facebook friends posted a quote of a result by Paul Erdös:

If an infinite set of points in the plane determines only integer distances, then all the points lie on a straight line.

When a mathematician reads something like this, after realizing that it is a nice result, the first question that comes to his mind is: is it possible to construct a finite set of n points in the plane that do not lie in a straight line, and whose distances are all integers?

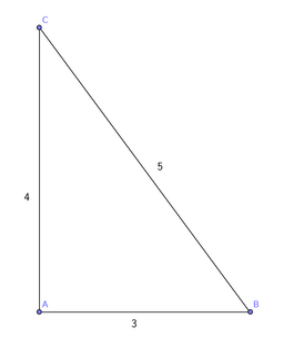
Well, it is easy to see that one can do that for n=3 (just consider any Pythagorean triple, such as the triangle with sides 3, 4, and 5). But is it possible to do that for an arbitrary n? The answer is not obvious at first, unless you have thought about the problem before (although that this is probably a very well established result). Actually, the proof of the statement above, called the Erdös-Anning theorem, was published in 1945, and the proof already contains a solution to the case with finitely many points. However, although beautiful, the example that the paper provides is overcomplicated, from my point of view.

Plus, I didn't know the answer to this question, and I realized that many of my fellows didn't know it either, so I started to try to construct examples of sets of non-aligned points with integer distances between them.

From the example of the triangle, it was easy to construct a set of n=4 points with this property, just by considering the rectangle of sides 3 and 4 (whose diagonal has length 5). But again, being able to do it for n=4 points doesn't mean that it can be done for any number of points, and I didn't see how to generalize that construction.

Read More