Plus, I didn't know the answer to this question, and I realized that many of my fellows didn't know it either, so I started to try to construct examples of sets of non-aligned points with integer distances between them.
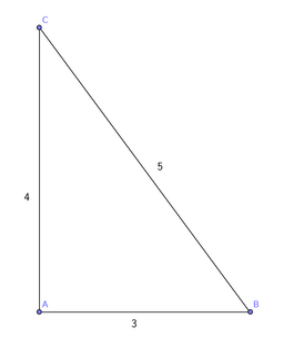
From the example of the triangle, it was easy to construct a set of n=4 points with this property, just by considering the rectangle of sides 3 and 4 (whose diagonal has length 5). But again, being able to do it for n=4 points doesn't mean that it can be done for any number of points, and I didn't see how to generalize that construction.
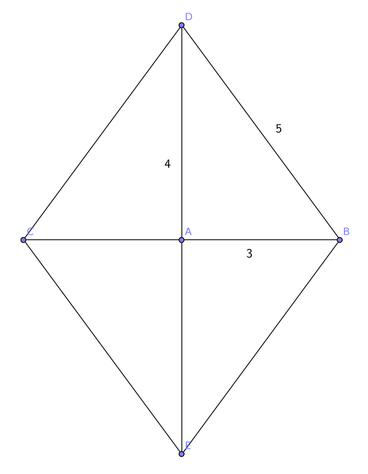
Hence I decided to come back to the idea of using Pythagorean triples, constructing some kind of symmetric set of points. I realized that an easy way to construct a set of n=5 points was by using four triangles with sides 3, 4, and 5 to form a rhombus with sides of length 5. The vertices of the rhombus together with the intersection of the two diagonals are a set of 5 points with the desired property.
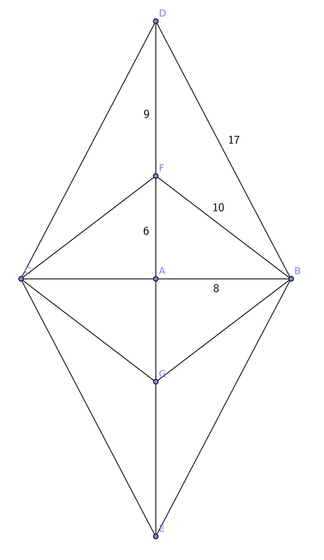
That's why I decided to try this construction with a rhombus build from four triangles with sides 8, 15, and 17. Since we want the distances x and l to be integer, when applying the Pythagorean theorem to the triangle with sides 8, l, and x, we get x²=l²+8², hence 8²=x²-l²=(x+l)(x-l), so we have to consider all the possible solutions where x+l and x-l are factors of 8²=64. It turns out that this system has one non-trivial solution for l=6 (hence x=10), so we can add two points in the big diagonal at distance 6 from the center, creating a set of n=7 points with the desired properties.
First of all, notice that any power of 2, say 2^k, is the length of the cathetus of a Pythagorean triangle, the Pythagorean triple being (2^(p+q+1), 2^(2p)-2^(2q), 2^(2p)+2^(2q)), where n=p+q+1 and p>q are integers. The way I came up with this triple is by using Euclid's formula to generate Pythagorean triples. Now, we can use the same method as before to add points in the cathetus of length 2^(2p)-2^(2q).
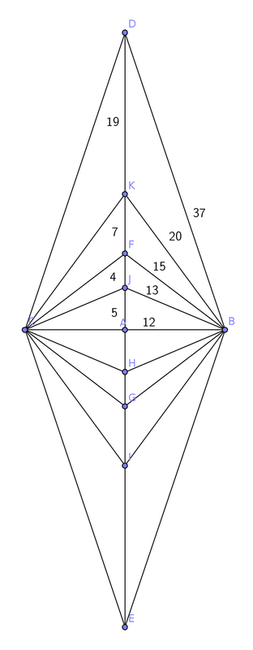
If a point is added at distance l from the center, and x represents de distance to the top (or the bottom) vertex, by the Pythagorean theorem we have 2^(2k)+l² = x², so we have the equation 2^(2k) = (x+l)(x-l). Since we want x and l to be integers, we have to solve the systems of equations x+l = 2^(2k-i), x-l=2^i, for i any integer between 0 and k (since we can assume x+l>x-l, restricting to l>0). This system always has a solution; however, some of the solutions are not valid for our purposes, namely when i=k (in which case l=0), when i=2q+1 (in which case we get a point that we already had), and when i=0 (in which case we get a non-integer). Hence, at the end of the day, we can add 2(k-2) points to the rhombus, which already has 5 points, so we get an example with n=2k+1 points. Of course, this is the case as long as all the solutions that we get are different; but this is something not too difficult to prove (you can see the details in the notes for the talk that I gave in the Math Club at UCR).
Hence, this proves that it is possible, using this construction, to get a set with any odd number of non-aligned points in the plain whose distances are integer numbers. By removing one of the points, we get the result for any even number of points, thus for any number.
After proving that, the Erdös-Anning theorem becomes even more interesting and mysterious!
| Notes_Talk_DiscoveringATheoremByErdos_MathClubUCR.pdf |
 RSS Feed
RSS Feed
