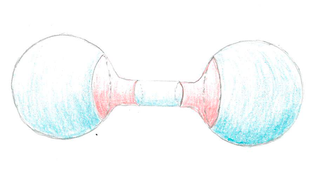
First introduced by Calabi, and also described by Cheeger in one of his famous papers, these dumbbell-shaped surfaces are a very well studied example in Spectral Geometry. The first eigenvalue of the Laplacian of these surfaces is proportional to the radius of the cylinder joining the two spheres. Thus, considering dumbbells with very thin cylinders, we obtain surfaces with arbitrarily small first eigenvalue.
In view of Lichnerowicz's theorem, this example shows that to find a positive lower bound for the first eigenvalue, one needs some kind of curvature assumption. Together with Kamryn Spinelli and Connor C. Anderson, two undergraduate students at Worcester Polytechnic Institute, we have been exploring this example in the context of integral curvature assumptions. Our exploration lead to a joint publication at PUMP Journal of Undergraduate Research, and the students presented our findings at the 2021 MAA MathFest and in the 2022 Joint Mathematics Meeting.
In view of Lichnerowicz's theorem, this example shows that to find a positive lower bound for the first eigenvalue, one needs some kind of curvature assumption. Together with Kamryn Spinelli and Connor C. Anderson, two undergraduate students at Worcester Polytechnic Institute, we have been exploring this example in the context of integral curvature assumptions. Our exploration lead to a joint publication at PUMP Journal of Undergraduate Research, and the students presented our findings at the 2021 MAA MathFest and in the 2022 Joint Mathematics Meeting.
Lichnerowicz's theorem and Zhong-Yang's theorem (sharpening an estimate of Li and Yau) give positive lower bounds for the first eigenvalue of the Laplacian for closed manifolds, assuming that the Ricci curvature is positive or non-negative. The pink regions in the dumbbell above contain negative curvature and are ultimately responsible for the lack of a lower bound.
In our joint article with Seto, Wei, and Zhang, we proved a Zhong-Yang type eigenvalue estimate for manifolds with a small amount of negative curvature (in an integral sense). Since the example above doesn't have a lower bound, it's clear that it must have a "large" amount of negative curvature (in integral sense). But is that amount uniformly bounded as we consider thinner and thinner cylinders? If so, this shows that "smallness" of the integral curvature is a necessary condition and can not be replaced by "bounded" integral curvature.
In our joint article with Seto, Wei, and Zhang, we proved a Zhong-Yang type eigenvalue estimate for manifolds with a small amount of negative curvature (in an integral sense). Since the example above doesn't have a lower bound, it's clear that it must have a "large" amount of negative curvature (in integral sense). But is that amount uniformly bounded as we consider thinner and thinner cylinders? If so, this shows that "smallness" of the integral curvature is a necessary condition and can not be replaced by "bounded" integral curvature.
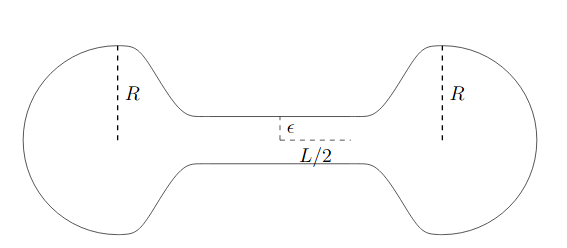
This is the question that we addressed with Spinelli and Anderson. We constructed explicitly a sequence of smooth dumbbell surfaces and estimated their integral curvature, showing that it remains uniformly bounded as the cylinders become thinner. Although this question had already been answered by Gallot, we approached the problem with the most elementary tools that we could find: an approach that doesn't require any background in the field. The main challenge was to find a way to smooth out a profile curve to generate a surface of revolution in such a way that we would be able to estimate the integral curvature afterwards.
After almost giving up a couple of times, and having tried several approaches, we managed to successfully construct the example explicitly. We wrote the result in an article that has been published by PUMP Journal of Undergraduate Research, and Spinelli and Anderson presented our findings during the 2021 MAA MathFest and in the 2022 Joint Mathematics Meeting. They are currently pursuing their PhD at Brandeis University and at Northeastern University.
 RSS Feed
RSS Feed
