Mathematics can be found everywhere: basic Arithmetic explains us how sales work, Differential Equations explain us how planets orbit around the Sun, Geometry tells us that the Earth is not flat, Combinatorics tells us how many "clinks" will we hear in a toast, Probability tells us how unlikely it is to become rich by buying lottery...
However, sometimes it is hard to explain what Algebra does for us (and here by Algebra I mean actual Algebra); and the truth is that Algebra is beneath every single one of these fields! In this post I want to explain one of my favourite theorems, how its roots are essentially algebraic (although it is a theorem in combinatorics), and how it can be applied to the real world: Pólya enumeration theorem.
However, sometimes it is hard to explain what Algebra does for us (and here by Algebra I mean actual Algebra); and the truth is that Algebra is beneath every single one of these fields! In this post I want to explain one of my favourite theorems, how its roots are essentially algebraic (although it is a theorem in combinatorics), and how it can be applied to the real world: Pólya enumeration theorem.
If I were to ask you in how many ways can you put in line 4 people, assuming that you have some basic notions of combinatorics, you are quickly going to say that you can do so in 4! =4·3·2·1 possible ways (we can choose the first person among 4 people, the second one among 3, the third one among 2, and then we are left with a single choice for the last one).
What happens, though, if I tell you instead that you want these 4 people to sit around a round table and that you want to know in how many different ways they can do so? Here the key point is what we mean by different: since the table is round, some different ways of arranging the 4 people in line become the same when they sit down around the table. For example, if these people are Alan, Berta, Claude, and Diana (A, B, C, D for short), then ABCD and BCDA are different ways of putting them in line, but when they sit around a round table in this order, the two give rise to the same way of sitting together. The reason is that in both situations, A is always sitting to the left of D, B is sitting to the left of A, C sits to the left of B, and D sits to the left of C (see the picture below).
What happens, though, if I tell you instead that you want these 4 people to sit around a round table and that you want to know in how many different ways they can do so? Here the key point is what we mean by different: since the table is round, some different ways of arranging the 4 people in line become the same when they sit down around the table. For example, if these people are Alan, Berta, Claude, and Diana (A, B, C, D for short), then ABCD and BCDA are different ways of putting them in line, but when they sit around a round table in this order, the two give rise to the same way of sitting together. The reason is that in both situations, A is always sitting to the left of D, B is sitting to the left of A, C sits to the left of B, and D sits to the left of C (see the picture below).
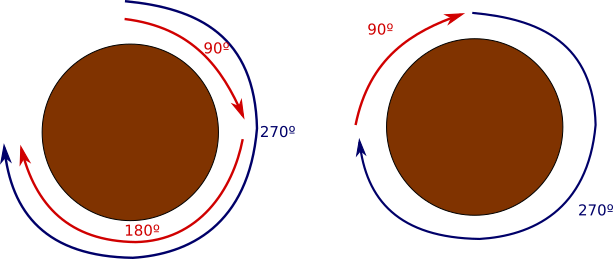
What's so different about the two problems? Well, in the latter, we are considering as the same solution situations that are related by a rotation; in other words, if you can arrange the people in two ways around the circle, but by rotating the first table you can get the second one, then we are saying that the two configurations are the same. In mathematics, when something like this happens, we say that there are symmetries associated to the problem.
And guess how mathematicians study symmetries? Using Algebra! Well, here is the thing: the symmetries associated to this problem are all the possible rotations of the table; however, around the table there are only 4 chairs, so basically we only care about the rotations that move one chair to the other, i.e. rotations of 0º, 90º, 180º, and 270º.
Notice that if we do two of these rotations, we always get another rotation; for example, a rotation of 90º followed by a rotation of 180º gives us a rotation of 270º. Also, every rotation has an inverse, i.e. a partner such that when we do both of them consecutively the result is the table that we had initially, as if we had not done any rotation at all; for example, a rotation of 270º followed by a rotation of 90º gives us a rotation of 360º which is the same as a rotation of 0º (i.e. no rotation at all).
And guess how mathematicians study symmetries? Using Algebra! Well, here is the thing: the symmetries associated to this problem are all the possible rotations of the table; however, around the table there are only 4 chairs, so basically we only care about the rotations that move one chair to the other, i.e. rotations of 0º, 90º, 180º, and 270º.
Notice that if we do two of these rotations, we always get another rotation; for example, a rotation of 90º followed by a rotation of 180º gives us a rotation of 270º. Also, every rotation has an inverse, i.e. a partner such that when we do both of them consecutively the result is the table that we had initially, as if we had not done any rotation at all; for example, a rotation of 270º followed by a rotation of 90º gives us a rotation of 360º which is the same as a rotation of 0º (i.e. no rotation at all).
When we have a set with these* properties, we say that the set is a Group. Algebra studies groups, among other mathematical structures; when a problem has symmetries, in most of the cases there is a group hidden somewhere. Groups are defined in a completely abstract way; in our case, the group in consideration is called the Cyclic group of order 4, which is a group generated by a single element (the rotation of 90º) such that when the element is applied 4 times in a row we get back to the initial configuration (and not before we apply it 4 times).
Although groups are very abstract: "sets with an operation that satisfies certain properties", all the finite groups can be thought of as a group of permutations (see Cayley's theorem for a precise statement). This means that we can always think of them as ways of rearranging a certain amount of elements. In the example above, the Cyclic group of order 4 can be thought as a group of permutations of 4 elements, i.e. elements of the Symmectric Group of 4 elements.
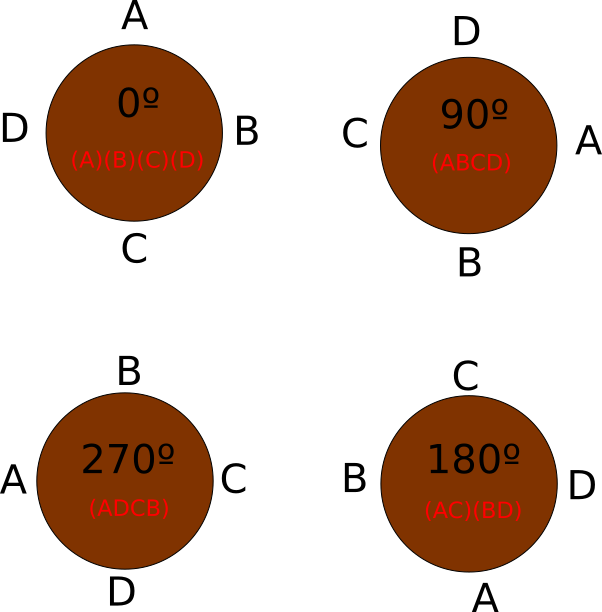
The advantage of thinking about the elements of the group as permutations is that this allows us to use the cycle notation. Consider the rotation of 90º in the example above. This rotation sends A to B, B to C, C to D, and D back to A; as a short notation, we can express this information as the permutation (ABCD), where each letter inside the parenthesis is sent to the letter to it's right (and the last letter in the parenthesis is sent to the first one, hence the name "cycle notation"). Similarly, we can represent the rotation of 180º as (AC)(BD), because, after a rotation of 180º, A takes the place of C and C takes the place of A (similarly for B and D). Notice that in this case, there are two independent cycles, both of length 2, while in the 90º case, there was only 1 cycle of length 4. The last two elements of the group are the rotation of 270º, which would be represented by (ADCB), which has again just 1 cycle of length 4, and the rotation of 0º, which would be represented by (A)(B)(C)(D), giving us 4 "cycles" of length 1.
Pólya's enumeration theorem uses precisely this information: take the group of symmetries G of your counting problem, and write its elements in cycle notation. Then count how many elements are there with each possible combination of cycle lengths, and use this information to construct the cycle index polynomial. In our case we have 2 elements with 1 cycle of length 4 (\(2x_4\)), 1 element with 2 cycles of length 2 (\(1x_2^2\) ), and 1 element with 4 cycles of length 1 (\(x_1^4\)). Dividing this by the order of the group, one gets the cycle index:
$$P(x_1,x_2,x_3,x_4) = \frac{1}{4}(2x_4+x_2^2+x_1^4)$$
$$P(x_1,x_2,x_3,x_4) = \frac{1}{4}(2x_4+x_2^2+x_1^4)$$
Now, this polynomial P is an algebraic object: it contains all the information about the symmetries of the problem, but it doesn't know what we want to count yet. At this point, we need to introduce the idea of "colorations". What we want to do is to "assign colors" to the different seats around the table (in our case, "labels" or "names"). We have 4 colors: A,B,C,D. We are not interested in any possible coloring, but only the colorings where each color appears exactly once. What we need to do to find out how many colorings are there of this sort, is to compute the polynomial:
$$F(a,b,c,d):=P(a+b+c+d, a^2+b^2+c^2+d^2, a^3+b^3+c^3+d^3, a^4+b^4+c^4+d^4)$$
where each variable \(a,b,c,d\) corresponds to one of the colors. The number in front of the monomial \(abcd\) will be the answer to our problem: the number of different colorings with each color appearing exactly once, taking into account the symmetries of the problem. In this case, expanding with the help of wolfram alpha (since the expansion has 35 terms) the polynomial:
$$F(a,b,c,d) = \frac{1}{4}((a+b+c+d)^4+(a^2+b^2+c^2+d^2)^2+2(a^4+b^4+c^4+d^4))$$
we see that the coefficient of \(abcd\) is 6. Hence, there are 6 possible ways of sitting around the table.
$$F(a,b,c,d):=P(a+b+c+d, a^2+b^2+c^2+d^2, a^3+b^3+c^3+d^3, a^4+b^4+c^4+d^4)$$
where each variable \(a,b,c,d\) corresponds to one of the colors. The number in front of the monomial \(abcd\) will be the answer to our problem: the number of different colorings with each color appearing exactly once, taking into account the symmetries of the problem. In this case, expanding with the help of wolfram alpha (since the expansion has 35 terms) the polynomial:
$$F(a,b,c,d) = \frac{1}{4}((a+b+c+d)^4+(a^2+b^2+c^2+d^2)^2+2(a^4+b^4+c^4+d^4))$$
we see that the coefficient of \(abcd\) is 6. Hence, there are 6 possible ways of sitting around the table.
In Spring 2017, I conducted an undergraduate research project on this topic (see the group pic that we took above). After understanding the theorem, we investigated several examples, showing how the cyclic index depends on the group action, and not only on the group of symmetries.
Because of its interdisciplinary flavour, between combinatorics and algebra, with applications to chemistry, graph theory, and statistical mechanics, it's a very attractive project for undergraduate students. I believe it could even be studied at an elementary level by high school students, at least in its simpler versions (like Burnside's lemma). In fact, in countries where students must write a research-like dissertation to finish high school (like in Catalonia), I think that this topic would be an exciting way of discovering modern mathematics, beyond the school level, helping to make an informed decision about whether to pursue a math degree in college.
Note: the problem that we have studied here under the scope of Pólya enumeration theorem didn't need such a powerful theorem to be solved. In fact, one can fix the position of A first, and then arrange the other 3 people in line, behind A. In other words, using a rotation, we can always make A sit on top; then we have to choose somebody that will sit to his right, which we can do in 3 possible ways, then choose somebody to sit in the bottom (2 possibilities), and somebody to sit to the left of A (only one person left). Hence, the solution is 3! = 6.
Note*: I wasn't careful in stating all the properties that a group should have; in particular, I left out associativity. For a more detailed definition, you can look at any book on Abstract Algebra, or even at Wikipedia.

 RSS Feed
RSS Feed
