
Last summer I participated in a summer school on Geometric Analysis in the beautiful town of Como, Italy. A part from having a great time and meeting a lot of mathematicians, I was introduced, by professor Christina Sormani (CUNY), to a new notion of convergence of metric spaces: the Sormani-Wenger Intrinsic Flat Convergence.
What is this all about, you might be asking? Well, before jumping on this rather involved concept, let's try to understand what is a metric space and what do I mean by convergence of metric spaces.
What is this all about, you might be asking? Well, before jumping on this rather involved concept, let's try to understand what is a metric space and what do I mean by convergence of metric spaces.
Geometry, as its name suggests, is the science of measuring things on Earth, i.e. quantifying the distance between objects. In modern mathematics, there are many different subfields under this name, and not all of them deal with the notion of distance. However, one of them, called Metric Geometry, remains having distance as its main object of study.
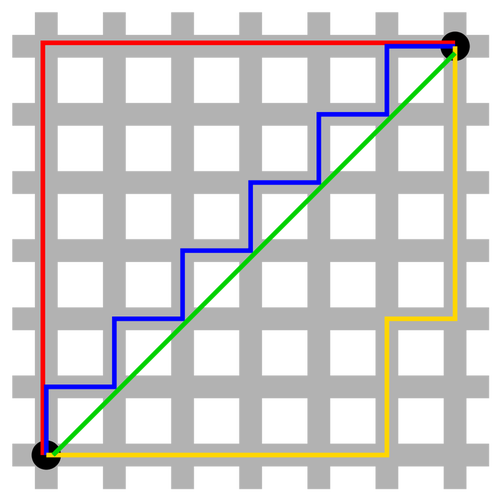
A set with a distance is called a Metric Space. There are many different examples of metric spaces: the most basic ones are the real line, the plane, or the three dimensional space with the usual (Euclidean) distances. However, these notions of distance are not always useful. For instance, if you are a taxi driver in Barcelona, and you want to know how far is Sagrada Família from Plaça de Catalunya, the usual distance between two points in the plane is not going to be the actual distance that you are going to drive, since cars, like humans, can not go through buildings. Instead, you will probably need to use the Taxicab distance, which computes the distance between two points on a grid, like the streets in l'Eixample of Barcelona.
A set with a distance is called a Metric Space. There are many different examples of metric spaces: the most basic ones are the real line, the plane, or the three dimensional space with the usual (Euclidean) distances. However, these notions of distance are not always useful. For instance, if you are a taxi driver in Barcelona, and you want to know how far is Sagrada Família from Plaça de Catalunya, the usual distance between two points in the plane is not going to be the actual distance that you are going to drive, since cars, like humans, can not go through buildings. Instead, you will probably need to use the Taxicab distance, which computes the distance between two points on a grid, like the streets in l'Eixample of Barcelona.
To be able to make sense of this new notion of distance in the plane, mathematicians needed to generalize the definition of distance; they did so by keeping only the key ingredients in the intuitive notion of distance:
Given a set S, a distance function in S is a map that assigns to each pair of points (elements in S) a number, and that satisfies:
Given a set S, a distance function in S is a map that assigns to each pair of points (elements in S) a number, and that satisfies:
- The distance between two points is always non-negative, and it is zero only when the two points are actually the same point.
- The distance between A and B is the same as the distance from B to A.
- The distance from A to C is, at most, the distance between A and a third point B plus the distance from B to C.
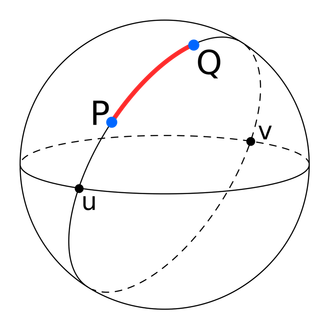
My favorite Metric Spaces are the so called Riemannian Manifolds. A manifold is a generalization of the notions of curve and surface: they are n-dimensional smooth spaces. If this idea scares you, just think of your favourite surface; for example, a sphere! We live in a spherical planet, and we talk about distances between cities. However, the distance that we are interested in is not the distance between the two cities in the 3-dimensional space where we live in (because to go from one city to the other we can not make a tunnel through the Earth!). Instead, we want to know the shortest distance between them when travelling on the surface of the Earth. This notion of distance is called Riemannian distance, or geodesic distance.
Notice that the definition of distance above is extremely general: it allows us to define distances in any set! For instance, one can define distance in a graph, or in a set of functions (see for example the distance induced by the uniform norm in the set of continuous functions).
Once a distance is specified in a set S, we can define the notion of convergence. You might be familiar with the notion of convergence of numbers: consider the sequence 1, 1/2, 1/3, 1/4, 1/5, ... ; we can write it in general as x_n = 1/n. It is a decreasing sequence of positive numbers which approaches x = 0 when n goes to infinity. What we mean by that is that the distance between x_n and x becomes as small as we want by picking n large enough.
Similarly, given a sequence of elements x_n in the metric space S (i.e. an enumerated collection of elements x_1, x_2, x_3, etc.), we say that the sequence converges to an element x of S if the distances from x_n to x are as small as we want, for n large enough.
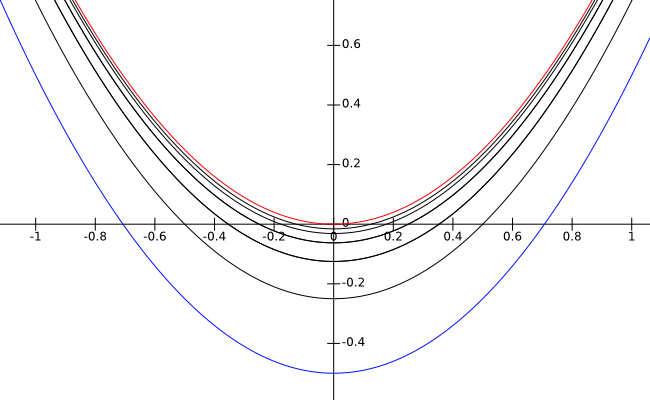
Different notions of distance give us different interpretations of convergence. In general, having a sequence x_n converging to an element x tells us that the elements x_n are becoming more and more similar to the element x (in some sense that changes depending on the chosen notion of distance!). For example, what does it mean that a sequence of functions f_n converges to f? In the uniform norm, this means that the functions f_n are approaching f at every point with "the same speed" (see the image below), i.e. uniformly in all the domain.
Once a distance is specified in a set S, we can define the notion of convergence. You might be familiar with the notion of convergence of numbers: consider the sequence 1, 1/2, 1/3, 1/4, 1/5, ... ; we can write it in general as x_n = 1/n. It is a decreasing sequence of positive numbers which approaches x = 0 when n goes to infinity. What we mean by that is that the distance between x_n and x becomes as small as we want by picking n large enough.
Similarly, given a sequence of elements x_n in the metric space S (i.e. an enumerated collection of elements x_1, x_2, x_3, etc.), we say that the sequence converges to an element x of S if the distances from x_n to x are as small as we want, for n large enough.
Different notions of distance give us different interpretations of convergence. In general, having a sequence x_n converging to an element x tells us that the elements x_n are becoming more and more similar to the element x (in some sense that changes depending on the chosen notion of distance!). For example, what does it mean that a sequence of functions f_n converges to f? In the uniform norm, this means that the functions f_n are approaching f at every point with "the same speed" (see the image below), i.e. uniformly in all the domain.
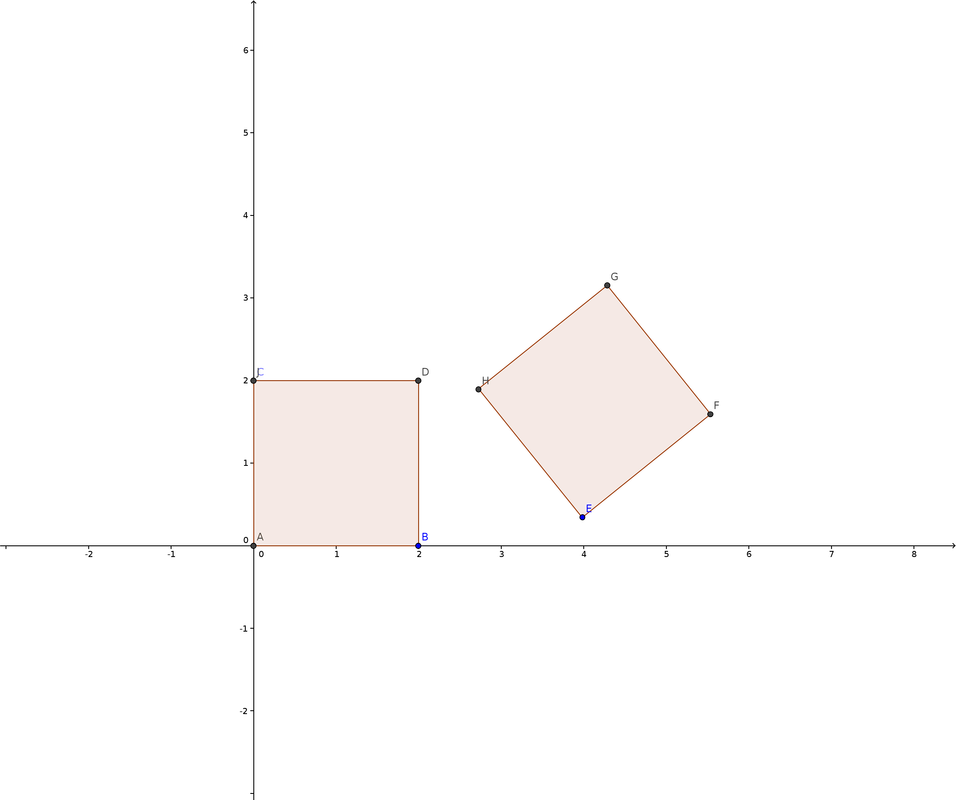
In metric geometry, one of the main concerns that we have is to know when two spaces X and Y are isometric. This means that one can get from one space to the other by a one to one and onto map that preserves distances (called an isometry). An example is illustrated in the picture below: consider X to be the square of vertices ABCD and Y to be the square with vertices EFGH. We can consider them as metric spaces (with the distance function inherited from the usual distance function in the plane). As sets, X and Y are completely different things (they contain different points). However, we can get from X to Y by using a rotation and a translation; rotations and translations preserve distances, hence X and Y are isometric as metric spaces.
In other words, two metric spaces are isometric if they are "the same" from the point of view of metric geometry (the two spaces in the example below are both squares of side 2, so in that sense, they are both "the same" object).
In other words, two metric spaces are isometric if they are "the same" from the point of view of metric geometry (the two spaces in the example below are both squares of side 2, so in that sense, they are both "the same" object).
Now, here is the key idea: wouldn't it be great if we could define a notion of distance between metric spaces in such a way that convergence in that distance means that the metric spaces are getting closer and closer to being isometric (i.e. being "the same" metric space)?
Yes, you heard me right: I am saying that it would be awesome to consider the space of all metric spaces, and to try to define a distance function in that space (so we would be measuring the distance between two metric spaces, not between the points in the metric space). The idea is that we could be asking ourselves what is the distance between any two sets where we have defined a distance: like the distance between the sphere and the plane.
Not only that, but we would like to define a notion of distance in such a way that two metric spaces are at distance zero exactly when they are "the same metric space" (i.e. isometric). So, for instance, the distance between a sphere and a plane would have to be always strictly positive, since these two spaces are not isometric.
This is exactly what the notion of Gromov-Hausdorff distance (first defined by M. Gromov, in the picture below, based on the Hausdorff distance) does: it defines a distance between any two (compact) metric spaces in such a way that the distance between two spaces is zero only when they are isometric.
Yes, you heard me right: I am saying that it would be awesome to consider the space of all metric spaces, and to try to define a distance function in that space (so we would be measuring the distance between two metric spaces, not between the points in the metric space). The idea is that we could be asking ourselves what is the distance between any two sets where we have defined a distance: like the distance between the sphere and the plane.
Not only that, but we would like to define a notion of distance in such a way that two metric spaces are at distance zero exactly when they are "the same metric space" (i.e. isometric). So, for instance, the distance between a sphere and a plane would have to be always strictly positive, since these two spaces are not isometric.
This is exactly what the notion of Gromov-Hausdorff distance (first defined by M. Gromov, in the picture below, based on the Hausdorff distance) does: it defines a distance between any two (compact) metric spaces in such a way that the distance between two spaces is zero only when they are isometric.
This notion of distance has been used a lot in the last 40 years, among other things, to study sequences of smooth manifolds and their limit spaces (this is what I do in my research!). For example, a sequence of spheres of radius 1/n converges in the Gromov-Hausdorff sense to a point. If we fix a point p in the sphere, and we study the points nearby (say the points at distance 1 from p), and then we let the radius of the sphere increase to infinity, it turns out that the sequence of neighborhoods of p converges to a neighborhood of a point in the flat plane in the Gromov-Hausdorff sense, i.e. a very large sphere is almost the same, as a metric space and near any fixed point, as a plane (that's why plane geometry works fine for our everyday lives, even if we live in a sphere!).
However, there are other sequences of metric spaces that we would like to converge in the GH sense (short for Gromov-Hausdorff) and that do not converge! Christina Sormani explains them very well in her article: consider a sphere with a smooth cusp. At every step, add more cusps, but make them thinner and thinner, always of the same length. After several steps, we get something that would look like a sea urchin. Tom Ilmanen proved that this sequence of "hairy spheres" (or sea urchins) does not converge to a sphere in the GH sense; however, he conjectured that the sequence should converge in some weak sense.
However, there are other sequences of metric spaces that we would like to converge in the GH sense (short for Gromov-Hausdorff) and that do not converge! Christina Sormani explains them very well in her article: consider a sphere with a smooth cusp. At every step, add more cusps, but make them thinner and thinner, always of the same length. After several steps, we get something that would look like a sea urchin. Tom Ilmanen proved that this sequence of "hairy spheres" (or sea urchins) does not converge to a sphere in the GH sense; however, he conjectured that the sequence should converge in some weak sense.
In 2010, Christina Sormani and Stefan Wenger came up with a new notion of convergence between (a special kind of) metric spaces, called the Intrinsic Flat Convergence, in which this sequence of hairy spheres converges to the usual sphere.
So to the question: is a sea urchin a ball? The answer depends on your metric, tell me how you measure distances, and I will tell you whether they are the same or not!
So to the question: is a sea urchin a ball? The answer depends on your metric, tell me how you measure distances, and I will tell you whether they are the same or not!



 RSS Feed
RSS Feed
