- Newtonian Mechanics (Galilean transformations, inertial observers...)
- Electromagnetism (Maxwell's equations)
- Thermodynamics / Classical statistical mechanics

- The laws of physics are the same for any inertial observer.
- The velocity of light, c, is a constant of nature.
- Space & time are not independent, they are together in a 4D space called spacetime.
However, Special Relativity has several weaknesses:
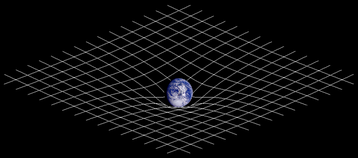
- It does not explain gravity: Newtonian gravity involves a vector field connecting instantaneously spacelike events (events separated by negative distances).
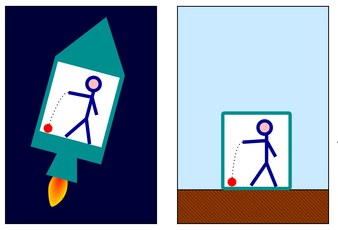
- How do we distinguish, a priori, between an inertial frame and a non-inertial frame?
On the left hand side we will have a tensor coming from geometry (the Einstein tensor), and on the right hand side we will have a tensor with the physical information (the Energy-Momentum tensor, already known in fluid mechanics). Einstein's tensor is constructed from Ricci's curvature tensor, the scalar curvature, and the metric. An additional term, proportional to the metric, can be added, but it is not considered as part as Einstein's tensor, since he refused to add this term, that would have as a consequence a non-static universe (if he had considered it, he would have been able to predict the expansion of the universe). Summarizing, Einstein's field equation looks as follows:
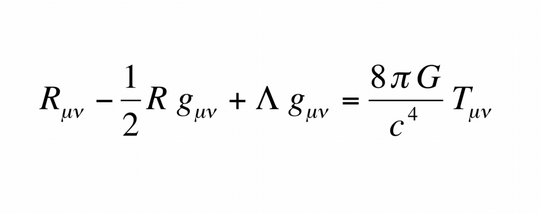
 RSS Feed
RSS Feed
